COM: bool_1_summary

COM: bool_1_intro

COM: BOOL_DEFS

ABS: 

ABS: tt

ABS: ff

STM: bool wf

STM: btrue wf

STM: bfalse wf

ABS: if b then t else f fi 

STM: ifthenelse wf

ABS: b

ABS: i <z j

STM: assert wf

STM: comb for assert wf

STM: lt int wf

ABS: b

ABS: p  q

ABS: p q

ABS: i z j

STM: btrue neq bfalse

STM: bnot wf

STM: band wf

STM: bor wf

STM: bor ff simp

STM: bor tt simp

STM: band ff simp

STM: band tt simp

STM: bnot bnot elim

STM: le int wf

STM: bnot thru band

STM: bnot thru bor

STM: bnot of le int

STM: bnot of lt int

ABS: b2i(b)

STM: b2i wf

STM: comb for b2i wf

STM: b2i bounds

STM: comb for bnot wf

STM: comb for bor wf

STM: comb for band wf

ABS: p =b q

STM: eq bool wf

ABS: p 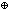b q

STM: bxor wf

ABS: p  q

STM: bimplies wf

STM: comb for bimplies wf

ABS: p  q

STM: rev bimplies wf

ABS: (i =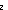 j)

STM: eq int wf

ABS: x =a y

STM: eq atom wf

COM: bool_thms

STM: bool cases

STM: bool ind

STM: decidable equal bool

STM: bimplies weakening

STM: bimplies transitivity

STM: assert functionality wrt bimplies

COM: bool_tactics_1

COM: assert_com

STM: assert of tt

STM: assert of ff

STM: assert elim

STM: not assert elim

STM: eqtt to assert

STM: eqff to assert

STM: decidable assert

STM: iff imp equal bool

STM: assert of eq atom

STM: assert of eq int

STM: neg assert of eq int

STM: neg assert of eq atom

STM: assert of lt int

COM: assert_eqint_rw

STM: assert of eq int rw

STM: assert of eq bool

STM: assert of bnot

STM: assert of band

STM: assert of bor

STM: assert of bimplies

STM: assert of le int

COM: bool_tactics

STM: ite rw test

STM: ite rw false

STM: ite rw true

STM: fun thru ite

COM: old_bool_1_stuff

STM: eq int eq false

STM: eq int eq true

STM: eq int eq false elim

STM: eq int eq true elim

STM: eq int cases test

STM: comb for lt int wf

COM: bool_1_end

Up	Standard, Standard